Сумма векторов - это основная операция векторной алгебры, результатом которой является новый вектор, полученный путем сложения соответствующих компонент исходных векторов. Эта операция подчиняется определенным математическим правилам и имеет важное значение в физике и технических науках.
Содержание
Геометрическое представление суммы векторов
Существует два основных способа геометрического сложения векторов:
- Правило треугольника - перенос начала второго вектора в конец первого
- Правило параллелограмма - построение параллелограмма на двух векторах как на сторонах
Алгебраическое сложение векторов
| Тип векторов | Формула сложения |
| На плоскости | a + b = (ax+bx, ay+by) |
| В пространстве | a + b = (ax+bx, ay+by, az+bz) |
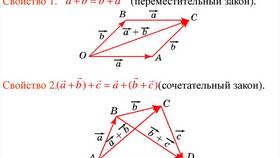
Свойства суммы векторов
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Существование нулевого вектора: a + 0 = a
- Существование противоположного вектора: a + (-a) = 0
Пример вычисления
Для векторов a = (2, -1, 3) и b = (-1, 4, 2):
- a + b = (2 + (-1), -1 + 4, 3 + 2) = (1, 3, 5)
Применение суммы векторов
- Физика: сложение сил, скоростей, ускорений
- Компьютерная графика: перемещение объектов
- Навигация: расчет результирующего направления
- Экономика: анализ многомерных данных
Особые случаи
| Случай | Результат |
| Коллинеарные векторы | Вектор того же направления |
| Перпендикулярные векторы | Диагональ прямоугольника |
| Противоположные векторы | Нулевой вектор |