Сумма внутренних углов любого треугольника в евклидовой геометрии всегда составляет 180 градусов. Это фундаментальное свойство является одной из базовых теорем геометрии и не зависит от вида или размеров треугольника.
Содержание
Сумма внутренних углов любого треугольника в евклидовой геометрии всегда составляет 180 градусов. Это фундаментальное свойство является одной из базовых теорем геометрии и не зависит от вида или размеров треугольника.
Доказательство теоремы о сумме углов
- Через вершину треугольника проводится прямая, параллельная противоположной стороне
- Образовавшиеся углы при вершине равны двум углам треугольника (как накрест лежащие)
- Развернутый угол (180°) состоит из трех углов: двух при вершине и одного угла треугольника
- Таким образом, сумма трех углов треугольника равна 180°
Примеры для разных типов треугольников
| Тип треугольника | Пример суммы углов |
| Равносторонний | 60° + 60° + 60° = 180° |
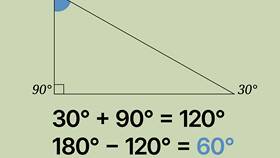
| Прямоугольный | 90° + 45° + 45° = 180° |
| Тупоугольный | 100° + 40° + 40° = 180° |
| Произвольный | 70° + 60° + 50° = 180° |
Исключения из правила
- В сферической геометрии сумма углов треугольника превышает 180°
- В геометрии Лобачевского (гиперболической) сумма углов меньше 180°
- На искривленных поверхностях классическая теорема не работает
Практическое применение теоремы
- Решение геометрических задач на вычисление углов
- Проверка правильности построения треугольников
- Конструирование и инженерные расчеты
- Компьютерная графика и 3D-моделирование
Историческая справка
Факт равенства суммы углов треугольника 180 градусам был известен еще древнегреческим математикам. Первое строгое доказательство этой теоремы приписывается Евклиду и содержится в его знаменитых "Началах" (III век до н.э.).
Знание этой теоремы является основополагающим для дальнейшего изучения геометрии и находит многочисленные применения в различных областях науки и техники.
