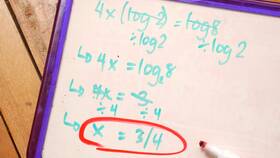Логарифмы представляют собой мощный математический инструмент, который находит применение в различных областях науки и техники благодаря своим уникальным свойствам и возможностям.
Содержание
Основные причины использования логарифмов
- Упрощение сложных вычислений
- Работа с экспоненциальными зависимостями
- Сжатие масштабов больших чисел
- Анализ данных с широким диапазоном значений
Области применения логарифмов
| Область | Применение | Пример |
| Математика | Решение уравнений | Показательные уравнения |
| Физика | Измерение интенсивностей | Шкала децибел |
| Химия | Расчет pH | Кислотность растворов |
| Экономика | Анализ роста | Сложные проценты |
Преимущества логарифмических преобразований
- Преобразование умножения в сложение
- Линеаризация экспоненциальных зависимостей
- Удобное представление очень больших и малых чисел
- Улучшение визуализации данных
Сравнение обычного и логарифмического масштабов
| Характеристика | Линейный масштаб | Логарифмический масштаб |
| Представление данных | Абсолютные значения | Относительные изменения |
| Диапазон значений | Ограниченный | Широкий |
| Визуализация роста | Линейная | Показывает кратность изменений |
Практическое применение в вычислениях
- Упрощение вычислений с большими числами
- Решение сложных показательных уравнений
- Анализ алгоритмической сложности
- Обработка сигналов и изображений
Историческое значение логарифмов
- Использовались для навигации и астрономии
- Легли в основу логарифмических линеек
- Ускорили научные расчеты до появления компьютеров
- Способствовали развитию математического анализа
Важные свойства логарифмов
- loga(xy) = logax + logay
- loga(x/y) = logax - logay
- loga(xn) = n·logax
- Формула перехода между основаниями
Логарифмы остаются важным математическим инструментом, который продолжает находить новые применения в современных технологиях и научных исследованиях, несмотря на развитие вычислительной техники.